LINÉAIRE ET MULTILINÉAIRE (ALGÈBRE)

LINЙAIRE ET MULTILINЙAIRE (ALGИBRE)

L’algèbre linéaire sur un corps commutatif, telle qu’on la trouvera présentée ici, s’est progressivement dégagée, au cours du XIX^e siècle et au début du XX^e, de la théorie des équations linéaires (systèmes de n équations linéaires à p inconnues, équations différentielles et intégrales linéaires) et de la géométrie (calcul vectoriel dans les espaces affines, transformations des espaces projectifs, dualité pour les sous-variétés linéaires et les quadriques, structure même de la géométrie). L’algèbre multilinéaire sur un corps commutatif a pris naissance dans la théorie des invariants et dans la partie de la géométrie différentielle consacrée au calcul tensoriel. Plus récemment, on a développé l’algèbre linéaire sur un anneau afin d’appliquer les méthodes de l’algèbre linéaire sur les corps à la théorie des groupes abéliens, considérés comme Z-modules, à la théorie des entiers algébriques sur un anneau commutatif unitaire, considérés comme éléments d’un module sur cet anneau, à la représentation linéaire d’un groupe dans un espace vectoriel, considéré comme module sur l’algèbre de ce groupe, et à l’étude des formes quadratiques sur Z. Enfin, ces dernières années ont été introduites l’algèbre homologique et, plus généralement, la théorie des catégories abéliennes, permettant d’appliquer la théorie des modules à des domaines où elle semblait inopérante (théorie des fibrés vectoriels et des faisceaux).

On trouvera un aperçu historique plus complet dans l’article ALGÈBRE. D’autre part, on trouvera des détails sur les applications de l’algèbre linéaire dans de nombreux articles tels que GROUPES (Mathématiques)-Groupes classiques et géométrie, Groupes de Lie et théorie des NOMBRES - Nombres algébriques. Bien entendu, la liste précédente n’est pas exhaustive: on pourrait, à la limite, affirmer que l’algèbre linéaire a envahi tous les domaines des mathématiques. À titre d’exemple, on consultera les applications à la théorie des équations algébriques (cf. CORPS [Mathématiques]) et à l’analyse fonctionnelle (cf. équations aux DÉRIVÉES PARTIELLES, DISTRIBUTIONS [Mathématiques], algèbres NORMÉES, espaces vectoriels NORMÉS).

Dans le présent article sera d’abord exposée la théorie des espaces vectoriels sur un corps commutatif, indépendamment de la notion de dimension. L’explicitation des résultats obtenus lorsque les espaces vectoriels sont de dimension finie et munis de bases fait l’objet du paragraphe consacré au calcul matriciel. Dans cette partie, l’exposé reste élémentaire, et la plupart des théorèmes sont accompagnés de démonstrations. Suivent quelques indications sur l’algèbre tensorielle et la théorie des modules.

En ce qui concerne la réduction des endomorphismes et la théorie des formes quadratiques, on se reportera aux articles: théorie SPECTRALE et formes QUADRATIQUES.

1. Espaces vectoriels et applications linéaires

Espaces vectoriels

Soit K un corps commutatif. On appelle espace vectoriel sur K, ou encore K-espace vectoriel, un ensemble E muni de deux lois de composition: une loi interne, application de E 憐 E dans E, notée (x , y ) 料 x + y et une loi externe, application de K 憐 E

dans K, notée ( 見, x ) 料 見 練 x , ou encore ( 見, x ) 料 見x ; ces deux lois satisfaisant aux conditions suivantes:

(a) L’ensemble E, muni de l’addition, est un groupe commutatif.

(b) Pour tout couple ( 見, 廓) d’éléments de K et pour tout élément x de E:

et, pour tout élément x de E, 1 練 x = x .

(c) Pour tout couple ( 見, 廓) d’éléments de K et pour tout couple (x , y ) d’éléments de E:

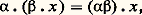
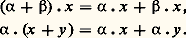Les éléments de E sont souvent appelés vecteurs , les éléments de K scalaires .

Applications linéaires

Soit E et F deux espaces vectoriels sur un même corps commutatif K. On dit qu’une application U de E dans F est K-linéaire ou, plus simplement, linéaire si, pour tout couple (x , y ) d’éléments de E et pour tout couple ( 見, 廓) de scalaires:

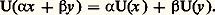On dit aussi que U est un morphisme d’espaces vectoriels.

Soit E, F et G trois espaces vectoriels sur K. Pour toute application linéaire U de E dans F et pour toute application linéaire V de F dans G, l’application composée V 獵 U est linéaire.

On dit qu’une application linéaire U de E dans F est un isomorphisme de E sur F s’il existe une application linéaire V de F dans E telle que:

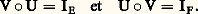Une application linéaire de E dans lui-même s’appelle endomorphisme de E, et un isomorphisme de E sur lui-même automorphisme de E.

Voici quelques exemples d’espaces vectoriels et d’applications linéaires:

1. Soit n un entier naturel non nul. L’ensemble Kⁿ des suites de n éléments de K, muni des deux lois définies par les formules:

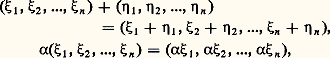est un espace vectoriel sur K.

2. Soit A un ensemble non vide et F un espace vectoriel sur K. L’ensemble ^A, noté encore 杻(A, F), des applications de A dans F, muni des deux lois définies par les formules:

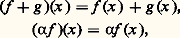est un espace vectoriel sur K.

3. Soit (Fⁱ )ⁱ size=1^捻I une famille d’espaces vectoriels sur un même corps commutatif K. L’ensemble produit :

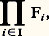muni des deux lois suivantes:

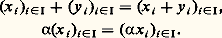est un espace vectoriel sur K, appelé espace vectoriel produit de la famille (Fⁱ )ⁱ size=1^捻I. (Lorsque tous les espaces vectoriels Fⁱ sont égaux à un même espace vectoriel F, l’espace produit n’est autre que ^I.) Pour tout élément j de I, le projecteur canonique de l’espace produit sur F^j , qui à toute famille (x ⁱ )ⁱ size=1^捻I associe le vecteur x ^j , est une application linéaire surjective.

4. Soit E un espace vectoriel sur K. On appelle forme linéaire sur E une application linéaire de E dans K, le corps K étant considéré comme espace vectoriel sur lui-même.

Par exemple, soit E l’espace vectoriel des fonctions continues sur l’intervalle [0,1] à valeurs complexes. L’application qui à tout élément f de E associe le scalaire:

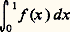est une forme linéaire sur E.

Sous-espaces vectoriels

Soit E un espace vectoriel sur K, (x ⁱ )ⁱ size=1^捻I une famille de vecteurs de E, ( 見ⁱ )ⁱ size=1^{捻 I} une famille de scalaires dont le support J est fini. (On appelle support de ( 見ⁱ )ⁱ size=1^{捻 I} l’ensemble J des éléments i de I tels que 見ⁱ 0.) Pour toute partie finie H de I contenant J:

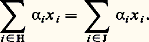Cette somme se note encore:

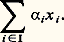Cette convention permet de poser la définition suivante: On dit qu’un vecteur x de E est combinaison linéaire des vecteurs x ⁱ s’il existe une famille ( 見ⁱ )ⁱ 捻^I de scalaires à support fini telle que:

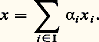Par exemple, soit E l’espace vectoriel des fonctions à valeurs réelles définies sur R, et (f ⁿ )ⁿ size=1^捻N la famille des fonctions monomiales f ⁿ : x 料 x ⁿ . Les combinaisons linéaires de ces fonctions ne sont autres que les fonctions polynomiales. En revanche, la fonction exponentielle x 料 e ^x n’est pas combinaison linéaire des fonctions f ⁿ .

Soit E un espace vectoriel sur K. On dit qu’une partie E de E est un sous-espace vectoriel de E si E est stable pour les deux lois de E et si, munie des lois induites, E est un espace vectoriel sur K.

Pour qu’une partie non vide E de E soit un sous-espace vectoriel de E, il faut et il suffit que, pour tout couple (x , y ) d’éléments de E et pour tout couple ( 見, 廓) de scalaires, le vecteur 見x + 廓y appartienne à E .

L’intersection d’une famille de sous-espaces vectoriels de E est encore un sous-espace vectoriel de E. Il en découle que, pour toute partie A de E, l’ensemble des sous-espaces vectoriels de E contenant A possède un plus petit élément (au sens de la relation d’inclusion), à savoir l’intersection de tous les sous-espaces vectoriels contenant A. Ce sous-espace vectoriel, dit engendré par A, est encore l’ensemble des combinaisons linéaires d’éléments de A, lorsque A est non vide. Voici quelques exemples.

Le sous-espace vectoriel engendré par un vecteur x est noté Kx ; c’est en effet l’ensemble des vecteurs de E de la forme 見x , où 見 appartient à K.

Soit E un espace vectoriel sur K et (Eⁱ )ⁱ size=1^{捻 I} une famille de sous-espaces vectoriels de E. Le sous-espace vectoriel de E engendré par la réunion des sous-espaces vectoriels Eⁱ est constitué des vecteurs de E de la forme:

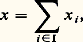où, pour tout élément i de I, x ⁱ appartient à Eⁱ , et où la famille (x ⁱ )ⁱ size=1^{捻 I} est à support fini. Ce sous-espace vectoriel s’appelle aussi somme des sous-espaces vectoriels Eⁱ , et se note:

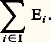Dans le cas particulier où I =1, 2, la somme des sous-espaces vectoriels E¹ et E² se note E¹ + E².

Espaces vectoriels d’applications linéaires

Soit E et F deux espaces vectoriels sur K. L’ensemble des applications linéaires de E dans F est un sous-espace vectoriel, noté 硫(E, F), de l’espace vectoriel 杻(E, F) des applications de E dans F.

Soit E, F et G trois espaces vectoriels sur K. L’application V 料 V 獵 U est une application linéaire de 硫(F, G) dans 硫(E, G), et l’application U 料 V 獵 U une application linéaire de 硫(E, F) dans 硫(E, G).

En particulier, l’ensemble des endomorphismes d’un espace vectoriel E, muni des trois lois de composition:

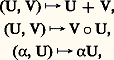est une algèbre associative unitaire, notée 硫(E) ^{[cf. ANNEAUX ET ALGÈBRES]}. Le produit V size=1^獵 U se note encore VU.

Les automorphismes de E constituent un groupe multiplicatif, appelé groupe linéaire de E, et noté GL(E); c’est le groupe multiplicatif des éléments inversibles de l’anneau unitaire 硫(E).

Factorisation des applications linéaires

Soit E et F deux espaces vectoriels sur K, et U une application linéaire de E dans F. L’image d’un sous-espace vectoriel de E par U est un sous-espace vectoriel de F. En particulier, l’image de E par U est un sous-espace vectoriel de F, appelé aussi image de U, et noté Im(U). De même, l’image réciproque d’un sous-espace vectoriel de F par U est un sous-espace vectoriel de E. En particulier, l’image réciproque du sous-espace vectoriel réduit au vecteur nul de F est un sous-espace vectoriel de E, appelé noyau de U, et noté Ker(U). Pour que U soit injective, il faut et il suffit que son noyau soit réduit au vecteur nul de E.

Théorème 1 (théorème de factorisation). Soit E, F et G: trois espaces vectoriels sur K.

1. Soit U une application linéaire surjective de E sur F. Pour toute application linéaire V de E dans G telle que Ker(V) contienne Ker(U), il existe une application linéaire W et une seule de F dans G telle que V = W 獵 U. Plus précisément, l’application W 料 W 獵 U est un isomorphisme de l’espace vectoriel 硫(F, G) sur le sous-espace vectoriel de 硫(E, G) constitué des applications linéaires dont le noyau contient celui de U.

2. Soit U une application linéaire injective de F dans G. Pour toute application linéaire V de E dans G telle que Im(V) soit contenue dans Im(U), il existe une application linéaire W et une seule de E dans F telle que V = U 獵 W. Plus précisément, l’application W 料 W 獵 U est un isomorphisme de l’espace vectoriel 硫(E, F) sur le sous-espace vectoriel de 硫(E, G) constitué des applications linéaires dont l’image est contenue dans celle de U.

Espaces vectoriels quotients

Soit E un sous-espace vectoriel d’un espace vectoriel E. La relation binaire dans E définie par les couples (x , y ) tels que x 漣 y appartienne à E est compatible avec les lois de E. Muni des lois quotients, l’ensemble quotient est un espace vectoriel sur K, appelé espace vectoriel quotient de E par E , et noté E/E . L’application canonique 﨏 de E sur E/E est linéaire, et son noyau est E .

Le théorème de factorisation montre aussitôt que le couple (E/E , 﨏) possède la propriété universelle suivante:

Pour tout couple (F, U) constitué d’un espace vectoriel F sur K et d’une application linéaire U de E dans F dont le noyau contient E , il existe une application linéaire U 黎 et une seule de E/E dans F telle que U = U 黎 獵 﨏. Plus précisément, l’application V 料 V 獵 﨏 est un isomorphisme de l’espace vectoriel 硫(E/E , F) sur le sous-espace vectoriel de 硫(E, F) constitué des applications linéaires de E dans F dont le noyau contient E .

Voici une conséquence immédiate de la propriété universelle des espaces vectoriels quotients: Soit E et F deux espaces vectoriels sur K, soit U une application linéaire de E dans F, soit 﨏 l’application canonique de E sur E/Ker(U), soit V l’unique application de E/Ker(U) dans Im(U) telle que U(x ) = (V 獵 﨏)(x ), pour tout vecteur x de E, et soit i l’injection canonique de Im(U) dans F. Alors V est un isomorphisme de E/Ker(U) sur Im(U), et:

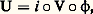formule de décomposition canonique de U, qui ramène en quelque sorte l’étude de U à celles de i , de 﨏 et de V.

Dualité

Soit E un espace vectoriel sur K. L’espace vectoriel 硫(E, K) des formes linéaires sur E s’appelle espace vectoriel dual de E, et se note E. L’application de E 憐 E dans K, qui au couple (y , x ) associe le scalaire y (x ), est une forme bilinéaire (cf. Bases ), dite canonique, et encore notée:

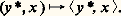Le dual de l’espace vectoriel E, c’est-à-dire l’espace vectoriel des formes linéaires sur E, s’appelle bidual de E, et se note E. Pour éviter des confusions, nous noterons:

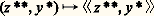la forme bilinéaire canonique sur E 憐 E..

Étant donné un vecteur x de E, l’application de E dans K, qui à toute forme linéaire y sur E associe le scalaire 麗y , x 礪, est une forme linéaire sur E; c’est donc un élément de E. L’application 﨑, qui associe au vecteur x cet élément de E, est une application linéaire de E dans E, dite canonique; elle est définie par la relation:

On dit qu’un vecteur x de E et une forme linéaire y sur E sont orthogonaux si 麗y , x 礪 = 0. On dit qu’une partie A de E et une partie B de E sont orthogonales si, pour tout élément x de A et pour tout élément y de B, x et y sont orthogonaux. L’ensemble des éléments de E orthogonaux à un sous-espace vectoriel F de E est un sous-espace vectoriel de E, appelé orthogonal de F, et noté F size=1^旅. De même, l’ensemble des vecteurs de E orthogonaux à un sous-espace vectoriel G de E est un sous-espace vectoriel de E, appelé orthogonal de G, et noté G .

Théorème 2 . Soit E et F deux espaces vectoriels sur K, soit E et F leurs duaux, et U une application linéaire de E dans F. Il existe une application linéaire de F dans E et une seule, appelée transposée de U et noté ^t U, telle que, pour tout élément x de E et pour tout élément y de F,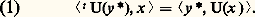

L’aplication ^t U n’est autre que l’application y 料 y 獵 U. La relation (1) s’appelle identité fondamentale de la transposition.

L’application U 料 ^t U est une application linéaire de 硫(E, F) dans 硫(F, E), appelée transposition.

La transposée de l’application identique de E n’est autre que l’application identique de son dual:

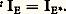Soit E, F et G trois espaces vectoriels sur K, soit U une application linéaire de E dans F, et V une application linéaire de F dans G. Alors la transposée de V 獵 U est égale à ^t U 獵 ^t V. En particulier, si G = E, et si U est inversible à gauche (resp. à droite), ^t U est inversible à droite (resp. à gauche). Plus particulièrement encore, si U est un isomorphisme de E sur F, ^t U est un isomorphisme de F sur E, et:

L’isomorphisme de E sur F ainsi défini s’appelle contragrédient de U, et se note face="EU Caron" U. Lorsque F = E, l’application U 料 face="EU Caron" U est un morphisme du groupe GL(E) dans le groupe GL(E).

Enfin, pour toute application linéaire U de E dans F, le noyau de ^t U n’est autre que l’orthogonal dans F de l’image de U:

Équations linéaires

Soit E et F deux espaces vectoriels sur K, soit U une application linéaire de E dans F, et b un élément de F. On appelle équation linéaire définie par U et b l’équation:

Le vecteur b s’appelle second membre de l’équation (1). Lorsque b = 0, on dit que l’équation (1) est homogène, ou, par abus de langage, sans second membre. L’équation:

s’appelle équation linéaire homogène associée à l’équation (1).

Voici les propriétés de l’ensemble des solutions d’une équation linéaire.

Si l’équation linéaire (1) est homogène, ses solutions constituent un sous-espace vectoriel de E, à savoir le noyau de U. Dans le cas général, si l’équation (1) admet une solution x ⁰, on obtient toutes les solutions de cette équation en ajoutant à x ⁰ une solution quelconque de l’équation homogène associée.

Enfin, pour que l’équation (1) admette une solution et une seule quel que soit le second membre b , il faut et il suffit que l’application linéaire U soit bijective, ou encore que sa transposée ^t U le soit. Dans ces conditions, l’unique solution de l’équation (1) n’est autre que U^-1(b ); l’application de F dans E, qui à tout vecteur b associe cette solution, est donc linéaire. On dit aussi que la solution dépend linéairement du second membre.

On voit donc que les notions d’image et de noyau sont fondamentales pour l’étude des équations linéaires.

2. Sommes directes, bases

Sommes directes

Soit (Eⁱ )ⁱ size=1^{捻 I} une famille d’espaces vectoriels sur K. Dans l’espace vectoriel: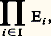

l’ensemble des éléments (x ⁱ )ⁱ 捻^I à support fini est un sous-espace vectoriel de cet espace vectoriel, appelé somme directe de la famille (Eⁱ )ⁱ size=1^{捻 I}, et noté:

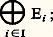il coïncide avec l’espace vectoriel produit lorsque l’ensemble I est fini.

Soit, en particulier, E un espace vectoriel sur K, soit (Eⁱ )ⁱ size=1^{捻 I} une famille de sous-espaces vectoriels de E, et U l’application linéaire de la somme directe de cette famille dans E qui à tout élément (x ⁱ )ⁱ size=1^{捻 I} associe l’élément:

Alors l’image de U est la somme: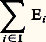

des sous-espaces vectoriels Eⁱ , et le noyau de U est l’ensemble des éléments (x ⁱ )ⁱ size=1^{捻 I} tels que:

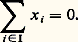Ainsi, pour que U soit surjective, il faut et il suffit que:

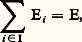et, pour que U soit injective, il faut et il suffit que, pour tout i 捻 I:

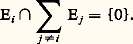Lorsque ces deux conditions sont réalisées, c’est-à-dire lorsque U est un isomorphisme, il est d’usage d’identifier E et:

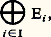ce qui conduit à dire que E est somme directe des sous-espaces vectoriels Eⁱ .

Enfin, pour que E soit somme directe des sous-espaces vectoriels Eⁱ , il faut et il suffit que tout vecteur x de E s’écrive d’une manière et d’une seule sous la forme:

où, pour tout élément i de I, x ⁱ appartient à Eⁱ .

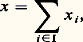L’intérêt de la notion de somme directe apparaît dans le théorème suivant.

Théorème 3. Soit E et F deux espaces vectoriels sur K, et (E^j )^j size=1^{殮 J} une famille de sous-espaces vectoriels de E dont E est somme directe.

1. Pour tout élément (U^j )^j size=1^{捻 J} de:

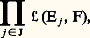il existe une application linéaire U et une seule de E dans F telle que, pour tout élément j de J, la restriction de U à E^j soit égale à U^j . À tout vecteur x de E, écrit sous la forme: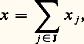

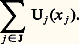où, pour tout j 捻 J, x ^j 捻 E^j , l’application U associe le vecteur:

2. L’application (U^j )^j size=1^{捻 J} 料 U est un isomorphisme de l’espace vectoriel:

sur l’espace vectoriel: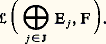

En particulier, deux applications linéaires de E dans F ayant, pour tout élément j de J, même restriction au sous-espace vectoriel E^j sont égales.

Sous-espaces vectoriels supplémentaires, projecteurs

On dit que deux sous-espaces vectoriels F et G d’un espace vectoriel E sur K sont supplémentaires dans E si les trois conditions équivalentes suivantes sont vérifiées:

(a) L’espace vectoriel E est somme directe de F et de G.

(b) Tout vecteur x de E s’écrit d’une manière et d’une seule sous la forme x = y + z , où y 捻 F et z 捻 G.

(c) La réunion de F et de G engendre E, et l’intersection de F et de G est réduite au vecteur nul.

L’application P^F qui associe au vecteur x le vecteur y est un endomorphisme de E, appelé projecteur sur F parallèlement à G. Le vecteur y est appelé projection de x sur F parallèlement à G. On définit de même P^G.

Le projecteur P^F a pour image F et pour noyau G, et les endomorphismes P^F et P^G satisfont aux relations:

Les seules relations P^F + P^G = I^E et P^F2 = P^F impliquent les relations (1) à (3). En effet P^FP^G = P^F(I^E 漣 P^F) = P^F 漣 P^F2 = 0; de même, P^GP^F = 0; enfin: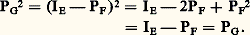

C’est pourquoi on dit qu’un endomorphisme U de E est un projecteur si U² = U. L’endomorphisme U est alors le projecteur sur Im(U) parallèlement à Ker(U).

Par exemple, dans l’espace vectoriel 杻(A, K) des applications d’un ensemble A dans K, le sous-espace vectoriel F des applications nulles en un point donné a de A et le sous-espace vectoriel G des applications constantes sont supplémentaires. Le projecteur sur G parallèlement à F est l’application f 料 f (a ).

De même, dans l’espace vectoriel sur C des fonctions n fois continûment dérivables sur R à valeurs complexes, le sous-espace vectoriel F des fonctions polynomiales de degré inférieur ou égal à n et le sous-espace vectoriel G constitué des fonctions f telles que, pour tout p 捻 [0, n ], (D^p f )(0) = 0 sont supplémentaires. Le projecteur sur F parallèlement à G n’est autre que l’application qui à toute fonction associe son développement limité à l’ordre n au point 0.

Soit enfin E un espace vectoriel sur K et (Eⁱ )ⁱ size=1^{捻 I} une famille de sous-espaces vectoriels de E dont E est somme directe. Pout tout élément i de I, l’application Pⁱ qui associe au vecteur x sa i -ième composante x ⁱ est le projecteur sur Eⁱ parallèlement à:

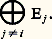La famille des projecteurs Pⁱ satisfait aux relations suivantes:

– Pour tout couple (i , j ) d’éléments distincts de I,

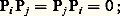– Pour tout élément i de I,

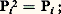– L’application identique de E est égale à la somme des projecteurs Pⁱ .

Une famille (Pⁱ )ⁱ size=1^{捻 I} de projecteurs de E satisfaisant aux trois conditions précédentes s’appelle système de projecteurs.

L’intérêt de la notion de sous-espaces vectoriels supplémentaires apparaît dans le théorème fondamental suivant.

Théorème 4. Soit E et F deux espaces vectoriels sur K, U une application linéaire de E dans F, E un sous-espace vectoriel de E, et U la restriction de U à E . Pour que U définisse un isomorphisme de E sur Im(U), il faut et il suffit que E soit un sous-espace vectoriel supplémentaire de Ker(U).

Soit en particulier E¹ un sous-espace vectoriel d’un espace vectoriel E sur K. Pour tout sous-espace vectoriel E² supplémentaire de E¹ dans E, la restriction à E² de l’application linéaire canonique de E sur E/E¹ est un isomorphisme de E² sur E/E¹. (Il suffit d’appliquer le théorème précédent au cas où F = E/E¹, où U est l’application linéaire canonique de E sur E/E¹, et où E = E².)

Soit enfin E² et E ² deux sous-espaces vectoriels supplémentaires de E¹ dans E. La restriction à E² du projecteur sur E ² parallèlement à E¹ définit un isomorphisme de E² sur E ². (Il suffit cette fois d’appliquer le théorème précédent au cas où F = E ², où U est le projecteur sur E ² parallèlement à E¹, et où E = E².)

Ainsi, deux sous-espaces vectoriels supplémentaires d’une même troisième sont canoniquement isomorphes.

Bases

Soit K^I l’espace vectoriel des applications d’un ensemble non vide I dans K. L’ensemble, noté K^(I), des applications de I dans K à support fini est un sous-espace vectoriel de K^I; il est égal à K^I si I est fini.

En particulier, prenons pour I l’ensemble N des entiers naturels. Alors K^N est l’espace vectoriel des séries formelles à coefficients dans K, tandis que K^(N) est l’espace vectoriel des polynômes à coefficients dans K.

On notera que:

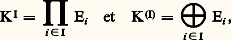où, pour tout élément i de I, Eⁱ = K. Par suite, l’espace vectoriel K^(I) est somme directe des sous-espaces vectoriels Ke ⁱ , où pour tout élément i de I, e ⁱ est l’élément de K^(I) défini par les formules e ⁱ (j ) = 嗀^ij . Autrement dit, tout élément f de K^(I) s’écrit d’une manière et d’une seule sous la forme:

où 見ⁱ n’est autre que f (i ).

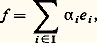Théorème 5. Le couple (K^(I), (e ⁱ )ⁱ size=1^{捻 I}) possède la propriété universelle suivante: Pour tout couple (E, (x ⁱ )ⁱ size=1^{捻 I}) constitué d’un espace vectoriel E sur K et d’une famille (x ⁱ )ⁱ size=1^{捻 I} de vecteurs de E, il existe une application linéaire U et une seule de K^(I) dans E telle que, pour tout élément i de I, U(e ⁱ ) = x ⁱ . L’application U associe à tout élément f = ( 見ⁱ )ⁱ size=1^{捻 I} le vecteur:

L’image de U est le sous-espace vectoriel de E engendré par les vecteurs x ⁱ , et le noyau de U est l’ensemble des éléments ( 見ⁱ )ⁱ size=1^{捻 I} tels que: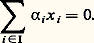

Les éléments de ce noyau sont appelés relations linéaires entre les vecteurs x ⁱ ; en particulier, le vecteur nul de K^(I) est appelé relation linéaire triviale entre ces vecteurs.

Ainsi, pour que U soit surjective, il faut et il suffit que tout vecteur x de E soit une combinaison linéaire des vecteurs x ⁱ . On dit alors que la famille (x ⁱ )ⁱ size=1^{捻 I} est génératrice . Pour que U soit injective, il faut et il suffit que toute relation linéaire entre les vecteurs x ⁱ soit triviale. On dit alors que la famille (x ⁱ )ⁱ size=1^{捻 I} est libre . Lorsque ces deux conditions sont réalisées, c’est-à-dire lorsque U est un isomorphisme de K^(I) sur E, on dit que la famille (x ⁱ )ⁱ size=1^{捻 I} est une base de E. Cela revient à dire que tout vecteur x de E peut s’écrire d’une manière et d’une seule sous la forme:

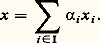La famille ( 見ⁱ )ⁱ size=1^{捻 I} s’appelle famille des composantes du vecteur x dans la base (x ⁱ )ⁱ size=1^{捻 I}.

Par exemple, la famille (e ⁱ )ⁱ size=1^{捻 I} est une base, dite canonique, de K^(I). En particulier, lorsque I = [1, n ], la base canonique de Kⁿ est constituée des n vecteurs suivants:

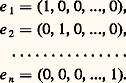De même, l’espace vectoriel K[X] = K^(N) des polynômes à une indéterminée à coefficients dans K a pour base canonique la famille des monômes e ⁿ = Xⁿ , où n parcourt N.

Soit S une partie de E. On dit que S est une partie génératrice, une partie libre ou une partie basique si la famille (x ^s )^s size=1^{捻 S}, où, pour tout élément s de S, x ^s = s , est une famille génératrice, une famille libre ou une base.

Pour qu’une partie à un seul élément x soit libre, il faut et il suffit que le vecteur x soit non nul. Lorsqu’une partiex , y à deux éléments n’est pas libre, on dit aussi que les vecteurs x et y sont colinéaires.

La notion de base permet d’exprimer sous la forme suivante la propriété universelle de l’espace vectoriel K^(I) énoncée dans le théorème 5.

Théorème 6. Soit E et F deux espaces vectoriels sur K, et (e ^j )^j size=1^{捻 J} une famille d’éléments de E. Si cette famille est génératrice, deux applications linéaires de E dans F prenant pour tout j 捻 J la même valeur sur le vecteur e ^j sont égales. Si cette famille est une base de E, pour toute famille (f ^j )^j size=1^捻J d’éléments de F, il existe une application linéaire U et une seule de E dans F telle que, pour tout j 捻 J, U(e ^j ) = f ^j . À tout vecteur x de E décomposé dans la base B sous la forme:

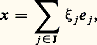l’application U associe le vecteur:

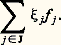Nous pouvons maintenant caractériser les applications linéaires injectives et surjectives à l’aide de la transformée d’une base.

Soit E et F deux espaces vectoriels sur K, soit U une application linéaire de E dans F, et (e ^j )^j size=1^{捻 J} une base de E. Pour que U soit surjective (resp. injective), il faut et il suffit que la famille (U(e ^j ))^j size=1^{捻 J} soit génératrice (resp. libre). Pour que U soit bijective, il faut et il suffit que (U(e ^j ))^j size=1^{捻 J} soit une base de F.

Lorsque F = K, le théorème 6 se particularise de la manière suivante.

Théorème 7. Soit E un espace vectoriel sur K, et B = (e ^j )^j size=1^{捻 J} une base de E. Pour toute famille ( 見^j )^j size=1^{捻 J} de scalaires, il existe une forme linéaire y et une seule sur E telle que, pour tout j 捻 J, 麗y , e ^j 礪 = 見^j . À tout vecteur x de E décomposé dans la base B sous la forme:

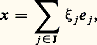la forme linéaire y associe le scalaire:

De plus, l’application ( 見^j )^j size=1^{捻 J} 料 y est un isomorphisme de l’espace vectoriel K^J sur l’espace vectoriel E.

Ainsi, le dual de K^(J) s’identifie à K^J, l’application bilinéaire canonique étant définie par la formule:

En particulier, pour tout entier naturel n , l’espace (Kⁿ ) est canoniquement isomorphe à Kⁿ .

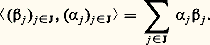3. Existence de bases

Théorème 8. Soit E un espace vectoriel sur K, soit L une partie libre de E, et S une partie génératrice de E contenant L. Il existe alors une partie basique B de E telle que L 說 B 說 S.

Nous allons démontrer ce théorème lorsque la partie S est finie.

Introduisons l’ensemble 劉 ordonné par inclusion des parties libres T de E telles que L 說 T 說 S. L’ensemble 劉 est non vide, puisque L appartient à 劉. La partie S étant finie, l’ensemble card(T) des entiers naturels, où T parcourt 劉, admet un plus grand élément p . Soit B un élément de 劉 ayant p éléments. Montrons que B convient. Puisque B appartient à 劉, la partie B est libre, et L 說 B 說 S. Il reste donc à prouver que B est génératrice. Supposons en effet par l’absurde que le sous-espace vectoriel E engendré par B ne soit pas égal à E. Puisque S est génératrice, il existe un élément x de S n’appartenant pas à E , ce qui implique que B = B 聆x est encore libre. Ainsi, B est un élément de 劉 ayant p + 1 éléments, ce qui contredit la définition de p .

Lorsque S est quelconque, la démonstration est analogue, le principe de récurrence étant remplacé par le théorème de Zorn.

Corollaire 1. Pour toute partie libre L de E, il existe une partie basique B de E contenant L; pour toute partie génératrice S de E, il existe une partie basique B de E contenue dans S. En particulier, pour tout espace vectoriel E sur K, l’ensemble des bases de E est non vide.

Ce corollaire s’obtient en spécialisant le théorème aux trois cas suivants: S = E, L = size=1^歷, S = E et L = size=1^歷.

Corollaire 2 (théorème de la base incomplète). Pour toute partie libre L de E et pour toute partie génératrice S de E, il existe une partie S de S telle que L 惡 S soit vide et que B = L 聆 S soit une partie basique de E.

Voici l’une des principales conséquences du théorème précédent:

Théorème 9. Tout sous-espace vectoriel E d’un espace vectoriel E admet un sous-espace vectoriel supplémentaire dans E.

On choisit en effet une partie basique B de E , que l’on complète en une partie basique B de E. Alors le sous-espace vectoriel engendré par B = B 漣 B est un sous-espace vectoriel supplémentaire de E dans E.

Corollaire 1. Soit E et F deux espaces vectoriels sur K, soit E un sous-espace vectoriel de E, et U une application linéaire de E dans F. Il existe alors une application linéaire U de E dans F prolongeant U .

Corollaire 2. Soit E et F deux espaces vectoriels sur K, soit F un sous-espace vectoriel de F, et 﨏 l’application linéaire canonique de F sur F/F . Pour toute application linéaire U de E dans F/F , il existe une application linéaire V de E dans F telle que U = 﨏 獵 V.

Corollaire 3. Soit E et F deux espaces vectoriels sur K, et U une application linéaire de E dans F. Pour que U soit surjective, il faut et il suffit que U soit inversible à droite, c’est-à-dire qu’il existe une application linéaire V de F dans E telle que U 獵 V = I^F. Pour que U soit injective, il faut et il suffit que U soit inversible à gauche, c’est-à-dire qu’il existe une application linéaire V de F dans E telle que V 獵 U = I^E.

En effet, il est évident que, si U est inversible à droite (resp. à gauche), U est surjective (resp. injective). Réciproquement, si U est surjective, U définit un isomorphisme U d’un supplémentaire E de Ker(U) sur F; il suffit de prendre pour V l’application linéaire de F dans E coïncidant avec U ^-1. De même, si U est injective, U définit un isomorphisme U de E sur Im(U); il suffit alors de prendre pour V l’application linéaire nulle sur un supplémentaire F de Im(U), et coïncidant avec U ^-1 sur Im(U).

4. Espaces vectoriels de dimension finie

Définition

On dit qu’un espace vectoriel E sur K est de dimension finie sur K, ou, plus simplement, de dimension finie, s’il existe une partie génératrice finie de E. Dans le cas contraire, on dit que E est de dimension infinie.

Pour qu’un espace vectoriel E soit de dimension finie, il faut et il suffit qu’il existe une partie basique finie de E, puisque de toute partie génératrice on peut extraire une partie basique.

Théorème 10. Soit E un espace vectoriel de dimension finie sur K, et B une partie basique finie de E ayant n éléments. Alors toute partie libre L de E est finie, et le nombre p d’éléments de L est inférieur ou égal à n . De plus, on peut compléter L en une partie basique de E en lui adjoignant (n 漣 p ) éléments convenablement choisis dans B.

Le théorème se démontre en utilisant le lemme d’échange suivant, qui fournit en outre un procédé pratique de complétion de L en une partie basique.

Lemme. Soit B = (e ¹, e ², ..., e ⁿ ) une base de E, soit q un entier inférieur ou égal à n , et L^q = (f ¹, f ², ..., f ^q ) une famille libre de E. On suppose que B ^q = (f ¹, f ², ..., f ^q-1 , e ^q , ..., e ⁿ ) est une base de E. Alors il existe au moins un entier i 捻 [q , n ] tel qu’en substituant f ^q à e ⁱ dans B^q on obtienne encore une base de E, notée B^q+1 .

Il suffit pour cela de décomposer f ^q dans la base B^q . Puisque L^q est libre, il existe au moins un entier i 捻 [q , n ] tel que la i -ième composante de f ^q soit non nulle. Il est alors immédiat que cet entier i convient.

Corollaire 1. Soit E un espace vectoriel de dimension finie sur K. Toutes les parties basiques de E sont finies, et elles ont le même nombre d’éléments.

Il résulte en effet du théorème 10 que toutes les parties basiques de E sont finies. Soit donc B et B deux parties basiques de E, ayant respectivement n et n éléments. Comme B est basique et que B est libre, n 諒 n ; de même, n 諒 n , et finalement n = n .

Le cardinal commun à toutes les parties basiques de E s’appelle dimension de E sur K, et se note dim^KE, ou, plus simplement, dim E. L’espace vectoriel réduit au vecteur nul est le seul espace vectoriel de dimension 0. Un espace vectoriel de dimension 1 s’appelle une droite , un espace vectoriel de dimension 2 s’appelle un plan.

Voici quelques exemples:

Soit I un ensemble non vide. L’espace vectoriel K^(I) est de dimension finie si et seulement si I est fini, et la dimension de K^(I) est alors égale à card(I). En particulier, pour tout entier naturel non nul n , Kⁿ est de dimension n .

Soit E et F deux espaces vectoriels sur K non réduits à0, soit B = (e ^j )^j size=1^{捻 J} une base de E, et B = (f ⁱ )ⁱ size=1^{捻 I} une base de F. Pour tout élément (i , j ) de I 憐 J, désignons par U^ij l’unique application linéaire de E dans F telle que, pour tout élément k de J,

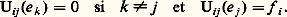Les applications linéaires U^ij constituent une base de l’espace vectoriel 硫(E, F), dite associée aux bases B et B . En particulier, si E et F sont de dimension finie, il en est de même de 硫(E, F), et:

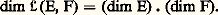(Notons que cette formule reste valable si E ou F est réduit à0.)

Plus particulièrement encore, l’espace vectoriel des endomorphismes de E est de dimension finie, et:

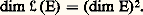Soit E un espace vectoriel sur K non réduit à0, et B = (e ^j )^j size=1^{捻 J} une base de E. Pour tout élément i de J, l’unique forme linéaire e ⁱ telle que, pour tout élément j de J:

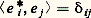s’appelle i -ième forme linéaire coordonnée. La famille (e ^j )^j size=1^{捻 J} des formes linéaires coordonnées est libre; pour que ce soit une base de E, il faut et il suffit que E soit de dimension finie. Cette base s’appelle base duale de la base B, et se note B. Nous voyons ainsi que l’espace vectoriel dual de E est de dimension finie si et seulement si E est de dimension finie, et que, dans ces conditions:

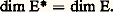Corollaire 2. Pour que deux espaces vectoriels de dimension finie sur K soient isomorphes, il faut et il suffit qu’ils aient même dimension.

Corollaire 3. Soit E un espace vectoriel de dimension finie n sur K, et S une partie génératrice finie de E. Alors le nombre p d’éléments de S est supérieur ou égal à n . De plus, il existe une partie basique de E constituée de n vecteurs convenablement choisis dans S.

Corollaire 4. Soit E un espace vectoriel de dimension finie n sur K. Toute partie libre de E ayant n éléments est une partie basique de E, et toute partie génératrice de E ayant n éléments est une partie basique de E.

Dimension et codimension d’un sous-espace vectoriel

Soit E un espace vectoriel sur K. On dit qu’un sous-espace vectoriel E de E est de codimension finie dans E si l’espace vectoriel quotient E/E est de dimension finie. La dimension de E/E s’appelle alors codimension de E dans E, et se note codim^EE . Les sous-espaces vectoriels de codimension 1 dans E s’appellent hyperplans de E.

Pour qu’un sous-espace vectoriel E de E soit de codimension finie dans E, il faut et il suffit que E admette un sous-espace vectoriel supplémentaire de dimension finie. Alors, pour tout sous-espace vectoriel E supplémentaire de E dans E:

Théorème 11. Soit E et F deux espaces vectoriels sur K, et U une application linéaire de E dans F.

1. Si F est de dimension finie et si U est injective, alors E est de dimension finie, et dim E 諒 dim F. En particulier, tout sous-espace vectoriel F d’un espace vectoriel F de dimension finie est aussi de dimension finie, et dim F 諒 dim F.

2. Si E est de dimension finie et si U est surjective, alors F est de dimension finie, et dim F 諒 dim E. En particulier, tout sous-espace vectoriel E d’un espace vectoriel E de dimension finie est de codimension finie dans E, et: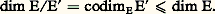

Soit en effet B une partie basique de E, et B une partie basique de E .

Si U est injective, card(U(B)) = card(B), et U(B) est une partie libre de F. Il résulte du théorème 10 que card(U(B)) 諒 card(B ). L’assertion 1 en découle, puisque F est de dimension finie. Le cas particulier s’en déduit en prenant pour E un sous-espace vectoriel F de F, et pour U l’injection canonique de F dans F.

Si U est surjective, U(B) est une partie génératrice de F; d’autre part, card (U(B)) 諒 card(B). Il résulte du corollaire 4 du théorème 10 que card(B ) 諒 card(U(B)). L’assertion 2 en découle, puisque E est de dimension finie. Le cas particulier s’en déduit en prenant pour F l’espace vectoriel quotient E/E , et pour U l’application linéaire canonique de E sur E/E .

Corollaire . Soit E un espace vectoriel de dimension finie sur K, et E un sous-espace vectoriel de E. Alors la dimension de tous les sous-espaces vectoriels supplémentaires de E dans E est égale à dim E 漣 dim E . De plus:

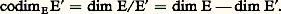En particulier, pour que E = E, il faut et il suffit que dim E = dim E. De même, les hyperplans d’un espace vectoriel de dimension n ne sont autres que les sous-espaces vectoriels de dimension n 漣 1.

Rang d’une application linéaire

Soit E et F deux espaces vectoriels sur K, et U une application linéaire de E dans F. On dit que U est de rang fini si l’image de U est un espace vectoriel de dimension finie. La dimension de Im(U) s’appelle alors rang de l’application linéaire U, et se note rang(U).

Théorème 12 . Pour que l’application linéaire U soit de rang fini, il faut et il suffit que le noyau de U soit de codimension finie dans E. Le rang de U est alors égal à la codimension dans E du noyau de U:

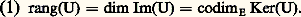En effet, l’espace vectoriel quotient E/Ker(U) est isomorphe à l’espace vectoriel Im(U).

Si F est de dimension finie, toute application linéaire U de E dans F est de rang fini, car Im(U), étant un sous-espace vectoriel de F, est de dimension finie.

Si E est de dimension finie, toute application linéaire U de E dans F est de dimension finie, et l’on a la formule de la dimension:

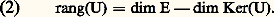En effet, U définissant une application linéaire surjective de E sur Im(U), l’espace vectoriel Im(U) est de dimension finie. La formule (2) est alors une conséquence de la formule (1) et de la suivante:

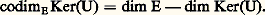Lorsque les espaces vectoriels E et F sont tous deux de dimension finie, et qu’ils ont même dimension n , il est équivalent de dire:

– L’application linéaire U est un isomorphisme de E sur F;

– L’application linéaire U est inversible à droite;

– L’application linéaire U est inversible à gauche;

– L’application linéaire U est bijective;

– L’application linéaire U est surjective;

– L’application linéaire U est injective;

– Le rang de U est égal à n .

Dualité en dimension finie

Théorème 13 . Soit E un espace vectoriel de dimension finie sur K. Alors l’application linéaire canonique 﨑 de E dans son bidual E est un isomorphisme.

Soit en effet x un élément du noyau de 﨑. Alors, pour toute forme linéaire y sur E,

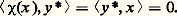Choisissons une base B = (e ^j )¹ size=1^諒j size=1^{諒 n} de E. En prenant successivement pour y les n formes linéaires coordonnées e ⁱ , nous voyons que toutes les composantes de x sont nulles, et donc que x = 0, ce qui montre que l’application linéaire 﨑 est injective. Comme:

la formule de la dimension permet d’en déduire que 﨑 est un isomorphisme de E sur E.

Il découle de ce théorème que l’application qui à toute base B de E associe sa base duale B est une bijection de l’ensemble des bases de E sur l’ensemble des bases de E.

On peut maintenant préciser les propriétés de l’orthogonalité en dimension finie.

Théorème 14 . Soit E un espace vectoriel de dimension finie sur K, et E son dual.

Pour tout sous-espace vectoriel F de E: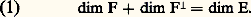

Pour tout sous-espace vectoriel G de E:

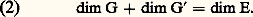De plus:

Considérons en effet une base (e ¹, e ², ..., e ^p ) de F, et complétons-la en une base (e ¹, e ², ..., e ⁿ ) de E; soit (e ¹, e ², ..., e ⁿ ) sa base duale. Pour établir la formule (1), il suffit de prouver que (e ^p+1 , e ^p+2 , ..., e ⁿ ) est une base de F size=1^旅. Les formes linéaires coordonnées e ^p+1 , e ^p+2 , ..., e ⁿ , appartiennent évidemment à F size=1^旅, car elles sont orthogonales aux vecteurs e ¹, e ², ..., e ^p , lesquels engendrent F; elles sont linéairement indépendantes, car elles font partie d’une base; enfin, il reste à montrer que tout élément y de F size=1^旅 est combinaison linéaire de ces éléments. Écrivons pour cela y sous la forme:

Puisque, pour tout élément i de [1, p ], 麗y , e ⁱ 礪 = 0, nous voyons que 兀¹ = 兀² = ... = 兀^p = 0, ce qui achève la démonstration. La formule (2) s’établit de manière analogue, en tenant compte du fait que toute base de E est la base duale d’une base de E. Enfin, la formule (3) se déduit des relations F 說 (F size=1^旅) , G 說 (G ) size=1^旅, dim F = dim(F size=1^旅) et dim G = dim(G ) size=1^旅, ces deux dernières égalités découlant des formules (1) et (2).

Théorème 15 . Soit E et F deux espaces vectoriels de dimension finie sur K, soit U une application linéaire de E dans F, et ^t U sa transposée.

Les applications linéaires U et ^t U ont même rang: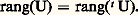

En effet, la formule de la dimension appliquée à ^t U montre que:

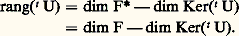D’autre part:

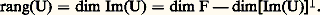La formule annoncée résulte alors du fait que le noyau de ^t U n’est autre que l’orthogonal de l’image de U.

5. Matrices

Matrices et applications linéaires

Soit E et F deux espaces vectoriels sur K non réduits à0, de dimensions respectives p et n , soit B = (e ¹, e ², ...., e ^p ) une base de E, soit B = (f ¹, f ², ..., f ⁿ) une base de F et U une application linéaire de E dans F. Pour tout élément j de [1, p ], le vecteur U(e ^j ) se décompose d’une manière et d’une seule dans la base B sous la forme:

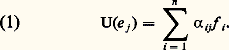Ainsi, à toute application linéaire U de E dans F nous pouvons associer une famille ( 見^ij ) d’éléments de K. Réciproquement, pour toute famille ( 見^ij ) d’éléments de K, où (i , j ) 捻 [1, n ] 憐 [1, p ], il existe une application linéaire U et une seule de E dans F satisfaisant aux conditions (1).

Nous sommes donc amené à introduire les définitions suivantes, utiles pour les calculs explicites concernant les applications linéaires: Soit K un corps commutatif, n et p deux entiers naturels non nuls. On appelle matrice à n lignes et p colonnes à éléments dans K toute famille:

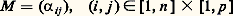d’éléments de K. Il est d’usage de disposer les éléments d’une matrice dans les cas d’un tableau rectangulaire à n lignes et p colonnes, encadré de deux parenthèses (ou parfois de deux crochets):

L’indice i s’appelle indice de ligne, l’indice j , indice de colonne. Pour tout élément i de [1, n ], la suite ( 見^ij )¹ size=1^諒j size=1^{諒 p} s’appelle i -ième ligne de M ; pour tout élément j de [1, p ], la suite ( 見^ij )¹ size=1^諒i size=1^{諒 n} s’appelle j -ième colonne de M .

Le vecteur de K^p dont les composantes constituent la i -ième ligne de M s’appelle i -ième ligne de M; le vecteur de Kⁿ dont les composantes constituent la j -ième colonne de M s’appelle j -ième vecteur colonne de M.

Lorsque n = 1, on dit que M est une matrice ligne; lorsque p = 1, on dit que M est une matrice colonne.

L’ensemble des matrices à n lignes et p colonnes à éléments dans K, se note Mⁿ ,^p (K). Lorsque n = p , on dit que M est une matrice carrée d’ordre n . L’ensemble des matrices carrées d’ordre n à éléments dans K se note Mⁿ (K).

Soit, plus généralement, A, I et J trois ensembles, I et J étant finis. On appelle matrice de type (I, J) à éléments dans A toute famille: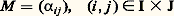

d’éléments de A. Lorsque I, ou J, est vide, on dit que M est la matrice vide.

Reprenons maintenant le problème initial: la matrice M = ( 見^ij ) définie par la formule (1) est dite associée à l’application linéaire U dans les bases B et B , et notée M ^B,B size=1(U). La matrice M a pour j -ième colonne la famille des composantes dans la base B de l’image par U du j -ième vecteur de la base B. L’application qui à toute application linéaire U de E dans F associe la matrice M ^B,B size=1(U) est une bijection de 硫(E, F) sur M^{n ,p} (K).

En particulier, lorsque E = F, U est un endomorphisme de E. La matrice M ^B,B size=1(U) est une matrice carrée, appelée matrice associée à l’endomorphisme U dans la base B, et notée plus simplement M ^B(U).

Toute matrice peut être considérée comme une matrice associée à une application linéaire: pour tout élément M de M^{n ,p} (K), il existe une application linéaire et une seule de l’espace vectoriel K^p dans l’espace vectoriel Kⁿ dont la matrice associée dans les bases canoniques de ces espaces vectoriels soit M . Cette application linéaire s’appelle application linéaire de K^p dans Kⁿ canoniquement associée à M.

Opérations sur les matrices

La bijection canonique 﨏 de Mn ,p (K) sur 硫(K^p , Kⁿ ) ainsi introduite conduit aux définitions qui suivent.

Somme de deux matrices . On appelle somme de deux éléments M = ( 見^ij ) et M = ( 見 ^ij ) de M^{n ,p} (K), et on note M + M , l’élément ( 廓^ij ) de M^{n ,p} (K) défini par les relations:

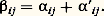Produit d’une matrice par un scalaire . On appelle produit d’un élément M = ( 見^ij ) de M^{n ,p} (K) par un scalaire, et on noteM , l’élément ( 廓^ij ) de M^{n ,p} (K) défini par les relations:

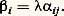Muni de ces deux lois, l’ensemble M^{n ,p} (K) est un espace vectoriel de dimension np sur K, et 﨏 est un isomorphisme de l’espace vectoriel M^{n ,p} (K) sur l’espace vectoriel 硫(K^p , Kⁿ ).

Plus généralement, soit E et F deux espaces vectoriels sur K, de dimensions respectives p et n , soit B une base de E, et B une base de F. La bijection U 料 M ^B,B size=1(U) est un isomorphisme de l’espace vectoriel 硫(E, F) sur l’espace vectoriel M^{n ,p} (K).

Produit de deux matrices . Soit m , n et p trois entiers naturels non nuls, soit M = ( 見^ij ) un élément de M^{n ,p} (K), et N = ( 廓^hi ) un élément de M^{m ,n} (K). On appelle produit des matrices M et N , et on note NM , l’élément ( 塚^hj ) de M^{m ,p} (K) défini par les relations:

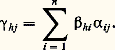On obtient donc l’élément 塚^hj à l’intersection de la h -ième ligne et de la h -ième colonne de NM en prenant la j -ième ligne de N , la j -ième colonne de M , et en ajoutant les produits des éléments de même indice (règle de multiplication «ligne par colonne»).

Grâce à la bijection canonique de M^{n ,p} (K) sur 硫(K^p , Kⁿ ), on voit aussitôt que, pour tout couple (M , M ) d’éléments de M^{n ,p} (K), pour tout couple (N , N ) d’éléments de M^{m ,n} (K) et pour tout couple (, 猪) de scalaires:

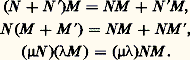Pour tout élément M de M^{n ,p} (K), pour tout élément N de M^{m ,n} (K) et pour tout élément P de M^{l ,m} (K),

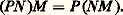Soit enfin E, F et G trois espaces vectoriels sur K, de dimensions respectives p , n et m , soit B une base de E, soit B une base de F, et B une base de G. Pour toute application linéaire U de E dans F et pour toute application linéaire V de F dans G:

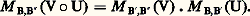Algèbre des matrices carrées d’ordre n . Muni des trois opérations précédentes, l’ensemble Mⁿ (K) est une algèbre associative unitaire. L’élément unité est la matrice:

Soit E un espace vectoriel sur K, et B une base de E. L’application U 料 M ^B(U) est un isomorphisme de l’algèbre unitaire 硫(E) sur l’algèbre unitaire Mⁿ (K). Dans cet isomorphisme, le groupe linéaire GL(E) a pour image le groupe, noté GLⁿ (K), ou encore GL(n , K), des matrices carrées d’ordre n inversibles. En particulier, si U est un automorphisme de E, M ^B(U) admet pour inverse la matrice associée à U^-1 dans la base B: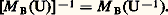

Transposée d’une matrice . Soit M un élément de M^{n ,p} (K). On appelle transposée de M , et on note ^t M , l’élément de M^{p ,n} (K) dont les colonnes sont les lignes de M .

Soit U l’application linéaire de K^p dans Kⁿ canoniquement associée à M ; alors ^t M n’est autre que la matrice associée à ^t U dans les bases canoniques de (Kⁿ ) et de (K^p ). Par suite, l’application M 料 ^t M est un isomorphisme de l’espace vectoriel M^{n ,p} (K) sur l’espace vectoriel M^{p ,n} (K). Pour tout élément M de M^{n ,p} (K) et pour tout élément N de M ^{m ,n} (K):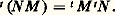

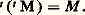Pour tout élément M de M^{n ,p} (K):

Soit enfin E et F deux espaces vectoriels sur K, de dimensions respectives p et n , soit B une base de E et B une base de F, soit B et B leurs bases duales. Pour toute application linéaire U de E dans F:

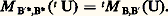Changement de base

Soit E un espace vectoriel de dimension p sur K. Considérons deux bases de E:

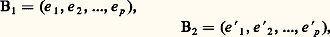appelées respectivement ancienne et nouvelle base. Pour tout élément j de [1, p ], le vecteur e ^j se décompose dans la base B¹ sous la forme:

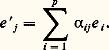L’élément P = ( 見^ij ) de M^p (K) s’appelle matrice de passage de la base B¹ à la base B²; ses colonnes sont constituées des composantes dans l’ancienne base des nouveaux vecteurs de base. La matrice P n’est autre que la matrice M ^B2,^B1(I^E) associée à l’application identique de E dans les bases B² et B¹. Il s’ensuit que la matrice P est inversible, et que la matrice de passage de B² à B¹ n’est autre que P ^-1.

Soit E et F deux espaces vectoriels non réduits à0 de dimension finie sur K, soit B¹ et B² deux bases de E et B ¹ et B ² deux bases de F, soit P la matrice de passage de B¹ à B² et Q la matrice de passage de B ¹ à B ². Pour toute application linéaire U de E dans F, les matrices associées à U dans les bases B¹ et B ¹, d’une part, et dans les bases B² et B ², d’autre part, sont liées par la relation:

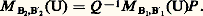En particulier, pour tout endomorphisme U de E:

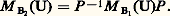Rang d’une matrice

Soit M un élément de M^{n ,p} (K). On appelle rang de la matrice M , et on note rang(M ) le rang de l’application linéaire de K^p dans Kⁿ canoniquement associée à M.

Plus généralement, soit E et F deux espaces vectoriels de dimension finie sur K non réduits à0, soit B une base de E et B une base de F. Pour toute application linéaire U de E dans F:

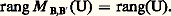De la relation entre le rang d’une application linéaire et celui de sa transposée, on déduit aussitôt que, pour tout élément M de M^{n ,p} (K):

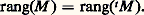Il en découle que le rang de M est égal au rang de ses vecteurs colonnes, ou encore au rang de ses vecteurs lignes.

Les caractérisations des applications linéaires inversibles conduisent à des caractérisations des matrices carrées inversibles.

Soit M un élément de Mⁿ (K). Il est équivalent de dire:

– La matrice M est inversible;

– La matrice M est inversible à droite;

– La matrice M est inversible à gauche;

– La matrice ^t M est inversible;

– Le rang de M est égal à n ;

– Le rang des vecteurs colonnes de M est égal à n ;

– Le rang des vecteurs lignes de M est égal à n .

Matrices équivalentes

Soit M ¹ et M ² deux éléments de M^{n ,p} (K). On dit que les matrices M ¹ et M ² sont équivalentes s’il existe deux matrices carrées inversibles P et Q d’ordres respectifs p et n à éléments dans K telles que:

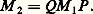Soit r un entier naturel. Pour qu’une matrice M de M^{n ,p} (K) soit de rang r , il faut et il suffit que M soit équivalente à la matrice J ^r = ( 見^ij ), où 見^ij = 1 si i 捻 [1, r ] et où 見^ij = 0 dans les autres cas.

Il en découle qu’une condition nécessaire et suffisante pour que deux éléments de M^{n ,p} (K) soient équivalents est qu’ils aient même rang.

On appelle opérations élémentaires les applications M 料 M de M^{n ,p} (K) dans lui-même de l’un des types suivants:

(a) La matrice M se déduit de la matrice M par permutation de deux colonnes, ou de deux lignes.

(b) La matrice M se déduit de la matrice M par multiplication d’une colonne, ou d’une ligne, par un scalaire non nul.

(c) La matrice M se déduit de la matrice M par addition à un vecteur colonne (resp. à un vecteur ligne) du produit d’un autre vecteur colonne (resp. d’un autre vecteur ligne) par un scalaire.

Pour que deux matrices M ¹ et M ² soient équivalentes, il faut et il suffit que l’on puisse transformer M ¹ en M ² par une suite finie d’opérations élémentaires.

La théorie des opérations élémentaires permet en outre de calculer le rang d’une matrice, son déterminant et, lorsqu’elle existe, la matrice inverse (cf. traitement numérique des MATRICES).

Systèmes d’équations linéaires

Soit n et p deux entiers naturels non nuls, U une application linéaire de K^p dans Kⁿ et M = ( 見^ij ) la matrice associée, soit a ¹, a ², ..., a ^p les vecteurs colonnes de cette matrice et a ¹, a ², ..., a ⁿ ses vecteurs lignes, soit enfin b = ( 廓ⁱ )¹ size=1^諒i size=1^{諒 n} un élément de Kⁿ . On désigne par x = ( 﨡^j )¹ size=1^諒j size=1^{諒 p} un élément de Kⁿ . L’équation U(x ) = b équivaut au système de n équations linéaires à p inconnues suivant:

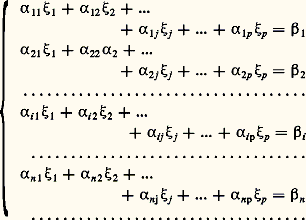La résolution de ce système peut s’interpréter vectoriellement comme la recherche des suites ( 﨡¹, 﨡², ..., 﨡^p ) de scalaires telles que:

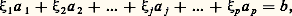ou encore comme la recherche des vecteurs x de K^p tels que:

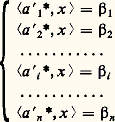c’est-à-dire des vecteurs x sur lesquels les formes linéaires a ¹, a ², ..., a ⁿ prennent des valeurs données 廓¹, 廓², ..., 廓ⁿ .

On appelle rang de ce système le rang de M, c’est-à-dire le rang de U. En appliquant les propriétés du rang des matrices, on obtient les résultats suivants:

Unicité des solutions . Il est équivalent de dire:

– Pour tout élément b de Kⁿ , l’équation U(x ) = b a au plus une solution;

– Les vecteurs colonnes a ¹, a ², ..., a ^p sont linéairement indépendants dans Kⁿ ;

– Les vecteurs lignes a ¹, a ², ..., a ⁿ engendrent (K^p );

– Le rang r de M est égal à p .

Existence des solutions quel que soit le second membre . Il est équivalent de dire:

– Pour tout élément b de Kⁿ , l’équation U(x ) a au moins une solution;

– Les vecteurs colonnes a ¹, a ², ..., a ^p engendrent Kⁿ ;

– Les vecteurs lignes a ¹, a ², ..., a ⁿ sont linéairement indépendants dans (K^p );

– Le rang r de M est égal à n .

Existence d’une solution, le second membre étant donné . Soit b un élément de Kⁿ . Il est équivalent de dire:

– L’équation U(x ) = b a au moins une solution;

– Le second membre b appartient au sous-espace vectoriel de Kⁿ engendré par a ¹, a ², ..., a ^p ;

– Le second membre b est orthogonal à Ker(^t U);

– Toute relation linéaire vérifiée par les vecteurs lignes l’est aussi par les composantes de b .

6. Applications multilinéaires

Définitions

Soit p un entier naturel non nul, soit E¹, E², ..., E^p et F des espaces vectoriels sur K. On dit qu’une application S de E¹ 憐 E² 憐 ... 憐 E^p dans F est multilinéaire , si, pour tout élément j de [1, p ], toute application partielle S^j de E^j dans F est linéaire. Lorsque F = K, on dit que S est une forme multilinéaire.

Soit E un espace vectoriel sur K. Les applications multilinéaires de E^p dans F s’appellent applications p -linéaires sur E à valeurs dans F, et les formes multilinéaires, formes p -linéaires.

Voici quelques cas particuliers:

Soit S une application p -linéaire sur E à valeurs dans F. On dit que S est alternée si, pour toute suite (x ¹, x ², ..., x ^p ) de vecteurs de E contenant deux vecteurs égaux:

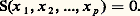On dit que S est symétrique si, pour toute permutation 靖 de [1, p ] et pour toute suite (x ¹, x ², ..., x ^p ) de vecteurs de E:

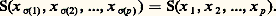On dit que S est antisymétrique si, dans les mêmes conditions:

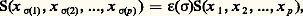où 﨎( 靖) désigne la signature de la permutation 靖.

Toute application p -linéaire alternée est antisymétrique; la réciproque devient vraie si la caractéristique du corps K est différente de 2.

Pour qu’une application p -linéaire S soit alternée, il faut et il suffit que, pour toute suite (x ¹, x ², ..., x ^p ) de vecteurs de E contenant deux vecteurs consécutifs x ⁱ et x ⁱ⁺¹ égaux:

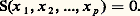Si S est alternée, on ne change pas la valeur de S sur une suite de p vecteurs de E en ajoutant à l’un de ces vecteurs une combinaison linéaire des autres. En particulier, si l’un des vecteurs x ¹, x ², ..., x ^p est une combinaison linéaire des autres, S(x ¹, x ², ..., x ^p ) = 0.

Les applications p -linéaires sur E à valeurs dans F constituent un sous-espace vectoriel, noté 紐^p (E, F), de l’espace vectoriel 杻(E^p , F) des applications de E^p dans F. Lorsque p = 1, 紐^p (E, F) n’est autre que 硫(E, F). Les applications p -linéaires symétriques et les applications p -linéaires alternées constituent des sous-espaces vectoriels de 紐^p (E, F), notés respectivement 崙^p (E, F) et 遼^p (E, F). Enfin, lorsque F = K, ces divers espaces vectoriels se notent plus simplement 紐^p (E), face=F0021 崙^p (E) et 遼^p (E).

Extension d’une application linéaire

Voici une généralisation de la transposition: Soit E, E et F trois espaces vectoriels sur K, et U une application linéaire de E dans E. Pour toute application p -linéaire S sur E à valeurs dans F, l’application S^U de E ^p dans F définie par la formule:

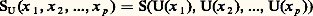est une application p -linéaire sur E à valeurs dans F. L’application U^p qui à tout élément S de 紐^p (E, F) associe S^U est une application linéaire de 紐^p (E, F) dans 紐^p (E , F), et l’image de U^p de 崙^p (E, F) (resp. de 遼^p (E, F)) est contenue dans 崙^p (E , F) (resp. dans 遼^p (E , F)). Soit enfin E un espace vectoriel sur K, et V une application linéaire de E dans E . Alors:

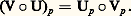Lorsque U est l’homothétie de rapport 見 dans l’espace vectoriel E, l’application U^p n’est autre que l’homothétie de rapport 見^p dans l’espace vectoriel 紐^p (E, F).

Voici maintenant une méthode générale de construction d’applications p -linéaires symétriques, ou alternées: Pour toute application p -linéaire S de E dans F, les applications M(S) et A(S) de E^p dans F, définies pour les formules:

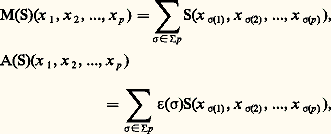où ^p désigne le groupe symétrique de degré p , sont respectivement symétrique et alternée. De plus, l’application M: S 料 M(S) de 紐^p (E, F) dans 崙^p (E, F) est linéaire, et l’application A: S 料 A(S) de 紐^p (E, F) dans 遼^p (E, F) est linéaire; elles se dénomment opérateurs de symétrisation et d’antisymétrisation.

Formes multilinéaires

Lorsque F = K, nous allons étudier la structure de 紐^p (E), de 崙^p (E) et de 遼^p (E).

Nous allons d’abord construire des formes p -linéaires à l’aide de formes linéaires.

Soit (y ¹, y ², ..., y ^p ) une suite de p formes linéaires sur E. L’application f de E^p dans K définie par la formule:

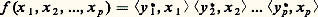est une forme p -linéaire sur E, appelée produit tensoriel des formes linéaires y ¹, y ², ..., y ^p et notée y ¹ 辰 y ² 辰 ... 辰 y ^p . Les applications M(f ) et A(f ), symétrisée et antisymétrisée de f , s’appellent respectivement produit symétrique et produit extérieur des formes linéaires y ¹, y ², ..., y ^p et se notent y ¹ 練 y ², ..., y ^p et y ¹ 廬 y ² 廬 ... 廬 y ^p .

L’application qui à (y ¹, y ², ..., y ^p ) associe y ¹ 辰 y ² 辰 ... 辰 y ^p (resp. y ¹ 練 y ² ... y ^p , resp. y ¹ 廬 y ² 礪 ... 廬 y ^p ) est une application p -linéaire (resp. p -linéaire symétrique, resp. p -linéaire alternée) de (E)^p dans 紐^p (E) (resp. dans 崙^p (E), resp. dans 遼^p (E)).

On dit qu’une forme p -linéaire S est un élément décomposable de 紐^p (E) (resp. de 崙^p (E), resp. de 遼^p (E)) s’il existe une suite (y ¹, y ², ..., y ^p ) de p formes linéaires sur E dont le produit tensoriel (resp. symétrique, resp. extérieur) est égal à S.

Il reste à montrer que toutes les formes p -linéaires peuvent être reconstituées à l’aide des éléments décomposables lorsque l’espace vectoriel E est de dimension finie, ce qui fait l’objet du théorème fondamental suivant.

Théorème 16 . Soit B = (e ¹, e ², ..., e ⁿ ) une base de E, et B = (e ¹, e ², ..., e ⁿ ) la base duale de B.

1. Soit 杻 l’ensemble des applications de [1, p ] dans [1, n ], et, pour tout élément 留 de 杻, e size=1^﨑 l’élément de 紐^p (E) défini par la formule:

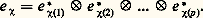Alors la famille (e size=1^﨑) size=1^﨑 size=1^捻 size=1^杻 est une basse de 紐^p (E), dite canoniquement associée à B. Par suite, la dimension de 紐^p (E) est égale à n ^p , et les formes p -linéaires décomposables constituent une partie génératrice de cet espace vectoriel. En particulier, l’espace vectoriel des formes bilinéaires sur E est de dimension n ².

2. Soit 崙 l’ensemble des applications s de [1, n ] dans N telles que:

et, pour tout élément s de 崙, e ^s l’élément de 崙^p (E) défini par la formule:

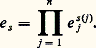Alors, si K est de caractéristique 0, la famille (e ^s )^s size=1^捻 size=1^崙 est une base de 崙^p (E), dite canoniquement associée à B. Par suite, la dimension de 崙^p (E) est égale à C^{p p+n-1} , et les formes p -linéaires symétriques décomposables constituent une partie génératrice de cet espace vectoriel. En particulier, l’espace vectoriel des formes bilinéaires symétriques sur E est de dimension n (n + 1)/2.

3. Lorsque p 礪 n , 遼^p (E) =0. Dans le cas contraire, soit 戮 l’ensemble des parties de [1, n ] à p éléments, et, pour tout élément P de 戮, e ^p l’élément de 遼^p (E) défini par la formule:

où 﨏 désigne l’application strictement croissante de [1, p ] dans (1, n ] ayant P pour image. Alors la famille (e ^p )^p size=1^捻 size=1^戮 est une base de 遼^p (E), dite canoniquement associée à B. Par suite, la dimension de 遼^p (E) est égale à C^{p n} , et les formes p -linéaires alternées décomposables constituent une partie génératrice de cet espace vectoriel. En particulier, l’espace vectoriel des formes bilinéaires alternées sur E est de dimension n (n 漣 1)/2.

Enfin, comme C^{n n} = 1, l’espace vectoriel des formes n -linéaires alternées sur E est de dimension 1, résultat dont l’importance va apparaître dans la théorie des déterminants.

En utilisant la structure de 遼^p (E), on établit facilement les deux critères d’indépendance linéaire suivants, très utiles en pratique.

Soit E un espace vectoriel de dimension n sur K, et p un entier inférieur ou égal à n . Pour qu’une suite (x ¹, x ², ..., x ^p ) de vecteurs de E soit libre, il faut et il suffit qu’il existe un élément f de 遼^p (E) tel que f (x ¹, x ², ..., x ^p ) 0. De même, pour qu’une suite (y ¹, y ², ..., y ^p ) de formes linéaires sur E soit libre, il faut et il suffit que y ¹ 廬 y ² 廬 ... 廬 y ^p 0.

7. Déterminants

Déterminant de n vecteurs

Soit E un espace vectoriel de dimension n sur K, et B = (e ¹, e ², ..., e ⁿ ) une base de E. La base de 遼ⁿ (E) canoniquement associée à B est réduite à la forme n -linéaire alternée e ¹ 廬 e ² 廬 ... 廬 e ⁿ ; celle-ci est la seule forme n -linéaire alternée sur E prenant la valeur 1 sur (e ¹, e ², ..., e ⁿ ). On l’appelle déterminant dans la base B, et on la note det^B. Pour tout élément f de 遼ⁿ (E) et pour toute suite (x ¹, x ², ..., x ⁿ ) de vecteurs de E: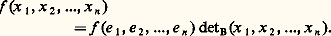

Les propriétés des formes n -linéaires alternées s’appliquent à det^B. De plus, le critère d’indépendance linéaire de n vecteurs s’énonce ici: pour que (x ¹, x ², ..., x ⁿ ) soit libre, il faut et il suffit que det^B(x ¹, x ², ..., x ⁿ ) 0.

Déterminant d’un endomorphisme

Soit E un espace vectoriel de dimension n sur K. Puisque 遼ⁿ (E) est de dimension 1, tout endomorphisme de 遼ⁿ (E) est une homothétie. En particulier, pour tout endomorphisme U de E, l’extension Uⁿ de U à l’espace vectoriel 遼ⁿ (E) est une homothétie; le rapport de cette homothétie s’appelle déterminant de l’endomorphisme U, et se note det U. Ainsi, par définition de det U, pour tout élément f de 遼ⁿ (E):

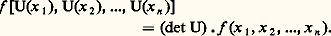Des propriétés des extensions des applications linéaires on déduit les résultats suivants:

– Pour tout couple (U, V) d’endomorphismes de E:

– Le déterminant de l’application identique de E est égal à 1; plus généralement, le déterminant de l’homothétie de rapport 見 est égal à 見ⁿ .

– Pour qu’un endomorphisme U de E soit inversible, il faut et il suffit que son déterminant soit non nul; dans ces conditions: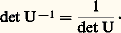

– Le déterminant du transposé ^t U d’un endomorphisme U de E est égal à celui de U:

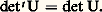L’application U 料 det U est donc un morphisme du groupe linéaire GL(E) dans le groupe multiplicatif K. Le noyau de ce morphisme est un sous-groupe distingué de GL(E), appelé groupe spécial linéaire de E, et noté SL(E).

Déterminant d’une matrice carrée

On appelle déterminant d’un élément M de Mⁿ (K), et on note det M le déterminant de l’endomorphisme de Kⁿ canoniquement associé à M . Les propriétés du déterminant d’un endomorphisme se transcrivent aussitôt pour les matrices. De plus, le déterminant de M n’est autre que le déterminant de ses vecteurs colonnes, ou de ses vecteurs lignes, dans la base canonique de Kⁿ . Enfin, les matrices de déterminant 1 constituent un sous-groupe distingué de GLⁿ (K), noté SLⁿ (K).

En utilisant la caractérisation du déterminant de n vecteurs, on démontre la proposition suivante: soit n et p deux entiers naturels non nuls tels que p 麗 n , soit A un élément de M^p (K), soit B un élément de M^n-p (K), soit C un élément de M^{p ,n} size=1^漣p (K), et M l’élément de Mⁿ (K) défini par la formule:

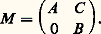Alors:

On peut en déduire la formule de développement d’un déterminant suivant une colonne, ou une ligne. Considérons pour cela un élément M = ( 見^ij ) de Mⁿ (K), où n 礪 1; pour tout couple (i , j ) d’éléments de [1, n ], notons A ^ij la matrice carrée d’ordre n 漣 1 obtenue en supprimant la i -ième ligne et la j -ième colonne de M . Alors, pour tout élément j de [1, n ]: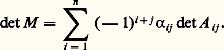

On est ainsi amené à considérer la matrice M dont les éléments 見 ^ij sont définis par la relation:

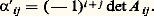La transposée de M s’appelle matrice complémentaire de M , et se note M 黎. Il en découle immédiatement que:

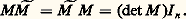En particulier, lorsque M est inversible:

formule dont le principal intérêt est de montrer que l’application M 料 M ^-1 est rationnelle.

8. Produits tensoriels

Produit tensoriel d’espaces vectoriels

La notion de produit tensoriel sert à remplacer l’étude des applications multinéaires par celle des applications linéaires. Plus précisément, on obtient le résultat suivant.

Théorème 17 . Soit E¹, E², ..., E^p des espaces vectoriels sur K. Il existe un couple (G, T) constitué d’un espace vectoriel G sur K et d’une application multilinéaire T de E¹ 憐 E² 憐 ... 憐 E^p dans G possédant la propriété universelle suivante: Pour tout couple (F, S) constitué d’un espace vectoriel F sur K et d’une application multilinéaire S de E¹ 憐 E² 憐 ... 憐 E^p dans F, il existe une application linéaire S 黎 et une seule de G dans F telle que S = S 黎 獵 T. Un tel couple (G,T) est unique à isomorphisme près. L’espace vectoriel G s’appelle produit tensoriel des espaces vectoriels E¹, E², ..., E^p , et se note E¹ 辰 E² 辰 ... 辰 E^p . L’application multilinéaire T se note: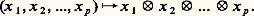

L’application S 料 S 黎 est un isomorphisme de l’espace vectoriel 紐(E¹ 憐 E² 憐 ... 憐 E^p , F) des applications multilinéaires de E¹ 憐 E² 憐 ... 憐 E^p dans F sur l’espace vectoriel 硫(E¹ 辰 E² 辰 ... 辰 E^p , F). Les éléments de E¹ 辰 E² 辰 ... 辰 E^p de la forme x ¹ 辰 x ² 辰 ... 辰 x ^p sont dits décomposables; ils constituent une partie génératrice de E¹ 辰 E² 辰 ... 辰 E^p . Si, pour tout élément j de [1, p ], E^j est de dimension finie n ^j et est muni d’une base B^j = (e ^ij ), alors les éléments e ⁱ¹ ,¹ 辰 e ⁱ² ,² 辰 ... 辰 e ^ip ,^p constituent une base de E¹ 辰 E² 辰 ... 辰 E^p , dite canoniquement associée aux bases B^j . En particulier:

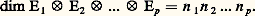Soit maintenant (E¹, E², ..., E^p ) et (F¹, ², ..., F^p ) deux suites d’espaces vectoriels sur K, et, pour tout élément j de [1, p ], U^j un élément de 硫(E^j , F^j ). Il existe alors une application linéaire U et une seule de E¹ 辰 E² 辰 ... 辰 E^p dans ¹ 辰 ² 辰 ... 辰 F^p telle que, pour tout élément (x ¹, x ², ... x ^p ) de E¹ 辰 E² 辰 ... 辰 E^p :

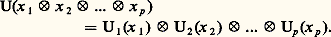On l’appelle produit tensoriel des applications linéaires U^j , et on la note U¹ 辰 U² 辰 ... 辰 U^p .

Trace d’un endomorphisme

Soit E et F deux espaces vectoriels sur K. Pour tout élément (a , b ) de E 憐 F, l’application U^{a ,b} qui à tout vecteur x de E associe le vecteur 麗a , x 礪 b de F est une application linéaire de E dans F; on l’appelle application linéaire élémentaire associée à (a , b ). Si a et b ne sont pas nuls, l’image de U^{a ,b} est la droite Kb de F, et son noyau est l’hyperplan de E noyau de la forme linéaire a . De plus, l’application (a , b ) 料 U^{a ,b} est une application bilinéaire de E 憐 F dans 硫(E, F).

Il existe une application linéaire j et une seule de E 辰 F dans 硫(E, F) telle que, pour tout élément (y , z ) de E 憐 F:

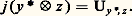En effet, l’application (y , z ) 料 U^{y ,z} est une application bilinéaire de E 憐 F dans 硫(E, F). La propriété universelle du produit tensoriel E 辰 F montre alors l’existence et l’unicité de j .

De plus, si E et F sont de dimension finie, j est un isomorphisme, car j est injective et que:

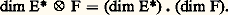Soit enfin E un espace vectoriel sur K. Il existe une forme linéaire c et une seule sur l’espace vectoriel E 辰 E telle que, pour tout élément (y , x ) de E 憐 E:

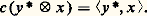L’application c s’appelle contraction canonique de E 辰 E dans K.

En effet, l’application (y , x ) 料 麗y , x 礪 est une application bilinéaire de E 憐 E dans K. La propriété universelle du produit tensoriel E 辰 E prouve l’existence et l’unicité de c .

En combinant les résultats précédents, nous obtenons le théorème qui suit.

Théorème 18. Soit E un espace vectoriel de dimension finie sur K. Il existe une forme linéaire et une seule sur l’espace vectoriel 硫(E), appelée trace et notée tr, telle que, pour tout endomorphisme élémentaire U^{a ,b} de E,

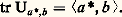Cette forme linéaire n’est autre que c 獵 j ^-1, où j désigne l’isomorphisme canonique de E 辰 E sur 硫(E).

De plus, la trace possède les propriétés suivantes:

– Pour tout couple (U, V) d’endomorphismes de E:

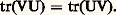– Pour tout endomorphisme U de E:

Enfin, on définit la trace d’un élément M = ( 見^ij ) de Mⁿ (K) comme la trace de l’endomorphisme de Kⁿ canoniquement associé à M ; on vérifie que: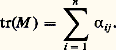

9. Modules

Soit A un anneau unitaire. On appelle A-module à gauche un ensemble E muni de deux lois de composition satisfaisant aux mêmes axiomes que les espaces vectoriels. On définit de même les A-modules à droite: cette fois

Par exemple, l’application (n , x ) 料 nx définit sur tout groupe abélien une structure de Z-module.

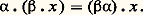Les résultats des chapitres 1 et 2 s’étendent sans changement dans ce cadre plus général, à ceci près que, lorsque l’anneau A n’est pas commutatif, les homothéties ne sont pas des endomorphismes, si bien qu’il n’est plus possible de munir le groupe additif 硫(E, F) d’une structure de A-module et l’anneau 硫(E) d’une structure de A-algèbre. Enfin, le dual d’un A-module à gauche doit être considéré comme un A-module à droite.

Existence de bases

Une différence essentielle avec les espaces vectoriels est la suivante: il peut arriver qu’une partie réduite à un élément non nul ne soit pas libre. C’est le cas pour les éléments de Z/n Z, considéré comme Z-module.

De plus, alors que, dans tout espace vectoriel, il existe des bases (cf. théorème 8), il n’en est pas de même dans tout module, même lorsqu’il existe une partie génératrice réduite à un seul élément; c’est le cas pour Z/n Z. Un module admettant une base est dit libre.

Existence de supplémentaires

De même, le théorème 9 ne se généralise pas à tous les modules. Ainsi, le sous-module du Z-module Z engendré par 2 n’admet pas de sous-module supplémentaire. Un sous-module admettant un supplémentaire est appelé facteur direct .

On dit qu’un A-module E est semi-simple si tout sous-module de E est un facteur direct. La théorie des modules semi-simples est utile pour la réduction des endomorphismes: Soit en effet U un endomorphisme d’un espace vectoriel E, et A le sous-anneau de 硫(E) engendré par U. L’application (V, x ) 料 V(x ) fait de E un A-module. Les sous-modules de E ne sont autres que les sous-espaces vectoriels de E stables par U. Pour que le module E soit semi-simple, il faut et il suffit que tout sous-espace vectoriel stable par U admette un supplémentaire stable. On dit alors que U est semi-simple.

Plus généralement, la théorie des modules semi-simples est utile pour la représentation linéaire des groupes (cf. GROUPES - Groupes de Lie), où elle intervient sous le nom de complète réductibilité.

Modules de type fini

On dit qu’un A-module E est de type fini s’il existe une partie génératrice finie de E. (Ici, la terminologie «de dimension finie» serait désastreuse, puisqu’un module de type fini peut très bien ne pas avoir de base.) Même lorsque E est un A-module libre de type fini, il peut arriver qu’il existe deux bases finies de E n’ayant pas le même nombre d’éléments. Cependant, ce phénomène ne se produit pas lorsque l’anneau A est commutatif.

On peut envisager deux généralisations «raisonnables» du théorème 11 concernant les sous-espaces vectoriels des espaces vectoriels de dimension finie:

1. Un sous-module d’un A-module de type fini n’est pas, en général, de type fini; c’est cependant le cas lorsque l’anneau A est noethérien. L’importance de ce cas apparaît dans la théorie des polynômes ^{[cf. ANNEAUX COMMUTATIFS]} et en géométrie algébrique.

2. Un sous-module d’un A-module libre n’est pas nécessairement libre; c’est cependant le cas lorsque l’anneau A est principal. Les résultats sont riches en applications pour la théorie des groupes abéliens et la réduction des endomorphismes, à propos des diviseurs élémentaires (cf. théorie SPECTRALE).

Applications multilinéaires et déterminants

Les résultats des chapitres 6 et 7 s’étendent sans changement au cas des A-modules libres de type fini sur un anneau commutatif, sauf les critères d’indépendance linéaire et d’inversibilité. En particulier, pour qu’un endomorphisme U soit inversible, il faut et il suffit que det U soit inversible dans l’anneau A. Ainsi modifié, ce critère d’inversibilité permet d’étudier les équations linéaires à coefficients entiers et, plus généralement, suivant les méthodes de Dedekind et de Kronecker, les entiers algébriques.

Encyclopédie Universelle. 2012.